Computational Examples in Matlab

In this section, we will take a look at some STFT filter-bank output signals when the input signal is a ``chirp.'' A chirp signal is generally defined as a sinusoid having a linearly changing frequency over time:

The matlab code is as follows:

N=10;           % number of filters = DFT length 
fs=1000;        % sampling frequency (arbitrary)
D=1;            % duration in seconds

L = ceil(fs*D)+1; % signal duration (samples)
n = 0:L-1;        % discrete-time axis (samples)
t = n/fs;         % discrete-time axis (sec)
x = chirp(t,0,D,fs/2);   % sine sweep from 0 Hz to fs/2 Hz
%x = echirp(t,0,D,fs/2); % for complex "analytic" chirp 
x = x(1:L);       % trim trailing zeros at end
h = ones(1,N);    % Simple DFT lowpass = rectangular window
%h = hamming(N);  % Better DFT lowpass = Hamming window
X = zeros(N,L);   % X will be the filter bank output
for k=1:N         % Loop over channels
  wk = 2*pi*(k-1)/N;
  xk = exp(-j*wk*n).* x;  % Modulation by complex exponential
  X(k,:) = filter(h,1,xk);
end

Figure 9.6 shows the input and output-signal real parts for a ten-channel DFT filter bank based on the rectangular window as derived above. The imaginary parts of the channel-filter output signals are similar so they're not shown. Notice how the amplitude envelope in each channel follows closely the amplitude response of the running-sum lowpass filter. This is more clearly seen when the absolute values of the output signals are viewed, as shown in Fig.9.7.

Figure 9.6: 10-Channel DFT filter bank real-chirp response. Output real part versus time in each channel (rectangular window).

Figure 9.7: 10-Channel DFT filter bank real-chirp response. Output magnitude versus time in each channel (rectangular window).

Replacing the rectangular window with the Hamming window gives much improved channel isolation at the cost of doubling the channel bandwidth, as shown in Fig.9.8. Now the window-transform side lobes (lowpass filter stop-band response) are not really visible to the eye. The intense ``beating'' near dc and half the sampling rate is caused by the fact that we used a real chirp. The matlab for this chirp boils down to the following:

function x = chirp(t,f0,t1,f1);
beta = (f1-f0)./t1;
x = cos(2*pi * ( 0.5* beta .* (t.^2) + f0*t));

x = exp(j*(2*pi * ( 0.5* beta .* (t.^2) + f0*t)));

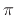Since our chirp frequency goes from zero to half the sampling rate, we are no longer exciting the negative-frequency channels. (To fully traverse the frequency axis with a complex chirp, we would need to sweep it from to .) We see in Fig.9.9 that there is indeed relatively little response in the ``negative-frequency channels'' for which 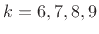, but there is some noticeable ``leakage'' from channel 0 into channel 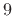, and channel 5 similarly leaks into channel 6. Since the channel pass-bands overlap approximately 75%, this is not unexpected. The automatic vertical scaling in the channel 7 and 8 plots shows clearly the side-lobe structure of the Hamming window. 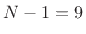Finally, notice also that the length start-up transient is visible in each channel output just after time 0.

Figure 9.8: Hamming-window DFT filter bank real-chirp response. Output magnitude versus time in each channel.

Figure 9.9: Hamming-window DFT filter bank analytic chirp response. Output magnitude versus time in each channel.