Hilbert Transform Design Example

We will now use the window method to design a complex bandpass filter which passes positive frequencies and rejects negative frequencies.

Since every real signal possesses a Hermitian spectrum 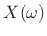, i.e., 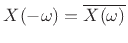, it follows that, if we filter out the negative frequencies, we will destroy this spectral symmetry, and the output signal will be complex for every nonzero real input signal (excluding dc and half the sampling rate). In other terms, we want a filter which produces a ``single sideband'' (SSB) output signal in response to any real input signal. The Hermitian spectrum of a real signal can be viewed as two sidebands about dc (with one sideband being the ``conjugate flip'' of the other). See §2.3.3 for a review of Fourier symmetry-properties for real signals.

An ``analytic signal'' in signal processing is defined as any signal having only positive or only negative frequencies, but not both (typically only positive frequencies). In principle, the imaginary part of an analytic signal is computed from its real part by the Hilbert transform (defined and discussed below). In other words, one can ``filter out'' the negative-frequency components of a signal by taking its Hilbert transform and forming the analytic signal . Thus, an alternative problem specification is to ask for a (real) filter which approximates the Hilbert transform as closely as possible for a given filter order.

• Primer on Hilbert Transform Theory
  • Hilbert Transform
  
  
• Preparing the Desired Impulse Response
  • Matlab, Continued
  • Kaiser Window
  • Hilbert Transformer by the Window Method
  
  
• More General FIR Filter Design
• Comparison to Optimal Chebyshev FIR Filter
• Conclusions