Next  |  Prev  |  Up  |  Top  |  Index  |  JOS Index  |  JOS Pubs  |  JOS Home  |  Search


Passive Reflectances

From Eq.(C.75), we have that the reflectance seen at a continuous-time impedance $ R(s)$ is given for force waves by

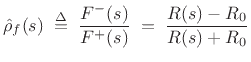$\displaystyle \hat{\rho}_f(s) \isdefs \frac{F^{-}(s)}{F^{+}(s)} \eqsp \frac{R(s)-R_0}{R(s)+R_0} \protect$ (C.76)

where $ R_0$ is the wave impedance connected to the impedance $ R(s)$ , and the corresponding velocity reflectance is $ \hat{\rho}_v(s)= -\hat{\rho}_f(s)$ . As mentioned above, all passive impedances are positive real. As shown in §C.11.2, $ R(s)$ is positive real if and only if $ \hat{\rho}_f(s)$ is stable and has magnitude less than or equal to $ 1$ on the $ j\omega $ axis (and hence over the entire left-half plane, by the maximum modulus theorem), i.e.,

$\displaystyle \left\vert\hat{\rho}_f(s)\right\vert \leq 1,$   re$\displaystyle \left\{s\right\} \leq 0. \protect$ (C.77)

In particular, $ \left\vert\hat{\rho}_f(j\omega)\right\vert \leq 1$ for all radian frequencies $ \omega\in(-\infty,\infty)$ . Any stable $ \hat{\rho}_f(s)$ satisfying Eq.(C.77) may be called a passive reflectance.

If the impedance $ R(s)$ goes to infinity (becomes rigid), then $ \hat{\rho}_f(s)$ approaches $ 1$ , a result which agrees with an analysis of rigid string terminations (p. [*]). Similarly, when the impedance goes to zero, $ \hat{\rho}_f(s)$ becomes $ -1$ , which agrees with the physics of a string with a free end. In acoustic stringed instruments, bridges are typically quite rigid, so that $ \hat{\rho}_f(j\omega)\approx 1$ for all $ \omega $ . If a body resonance is strongly coupled through the bridge, $ \vert\hat{\rho}_f(j\omega_c)\vert$ can be significantly smaller than 1 at the resonant frequency $ \omega_c$ .

Solving for $ R(s)$ in Eq.(C.77), we can characterize every impedance in terms of its reflectance:

$\displaystyle R(s) = R_0\frac{1+\hat{\rho}_f(s)}{1-\hat{\rho}_f(s)} $

Rewriting Eq.(C.76) in the form

$\displaystyle \hat{\rho}_f(s) \eqsp \frac{\dfrac{R(s)}{R_0}-1}{\dfrac{R(s)}{R_0}+1}, $

we see that the reflectance is determined by the ratio of the ``new impedance'' $ R(s)$ to the ``old'' impedance $ R_0$ in which the incoming waves travel. In other words, the incoming waves see the wave impedance ``step'' from $ R_0$ to $ R(s)$ , which results in a ``scattering'' of the incident wave into reflected and transmitted components, as discussed in §C.8. The reflection and transmission coefficients depend on frequency when $ R(j\omega)$ is not constant with respect to $ \omega $ .

In the discrete-time case, which may be related to the continuous-time case by the bilinear transform (§7.3.2), we have the same basic relations, but in the $ z$ plane:

$\displaystyle \hat{\rho}_f(z)$ $\displaystyle \isdef$ $\displaystyle \frac{F^{-}(z)}{F^{+}(z)} \eqsp \frac{R(z)-R_0}{R(z)+R_0}$  
$\displaystyle R(z)$ $\displaystyle =$ $\displaystyle R_0\frac{1+\hat{\rho}_f(z)}{1-\hat{\rho}_f(z)}$  
$\displaystyle \Gamma(z)$ $\displaystyle =$ $\displaystyle \Gamma _0\frac{1-\hat{\rho}_f(z)}{1+\hat{\rho}_f(z)} \protect$ (C.78)

where $ \Gamma\isdef 1/R$ denotes admittance, with

$\displaystyle \left\vert\hat{\rho}_f(z)\right\vert \leq 1, \quad \left\vert z\right\vert \leq 1. \protect$ (C.79)

Mathematically, any stable transfer function having these properties may be called a Schur function. Thus, the discrete-time reflectance $ \hat{\rho}_f(z)$ of an impedance $ R(z)$ is a Schur function if and only if the impedance is passive (positive real).

Note that Eq.(C.79) may be obtained from the general formula for scattering at a loaded waveguide junction for the case of a single waveguide ($ N=1$ ) terminated by a lumped load (§C.12).

In the limit as damping goes to zero (all poles of $ R(z)$ converge to the unit circle), the reflectance $ \hat{\rho}_f(z)$ becomes a digital allpass filter. Similarly, $ \hat{\rho}_f(s)$ becomes a continuous-time allpass filter as the poles of $ R(s)$ approach the $ j\omega $ axis.

Recalling that a lossless impedance is called a reactance (§7.1), we can say that every reactance gives rise to an allpass reflectance. Thus, for example, waves reflecting off a mass at the end of a vibrating string will be allpass filtered, because the driving-point impedance of a mass ($ R(s)=ms$ ) is a pure reactance. In particular, the force-wave reflectance of a mass $ m$ terminating an ideal string having wave impedance $ R_0$ is $ \hat{\rho}_f(s)= (ms-R_0)/(ms+R_0)$ , which is a continuous-time allpass filter having a pole at $ s=-R_0/m$ and a zero at $ s=R_0/m$ .

It is intuitively reasonable that a passive reflection gain cannot exceed $ 1$ at any frequency (i.e., the reflectance is a Schur filter, as defined in Eq.(C.79)). It is also reasonable that lossless reflection would have a gain of 1 (i.e., it is allpass).

Note that reflection filters always have an equal number of poles and zeros, as can be seen from Eq.(C.76) above. This property is preserved by the bilinear transform, so it holds in both the continuous- and discrete-time cases.


Subsections
Next  |  Prev  |  Up  |  Top  |  Index  |  JOS Index  |  JOS Pubs  |  JOS Home  |  Search
[How to cite this work]  [Order a printed hardcopy]  [Comment on this page via email]
``Physical Audio Signal Processing'', by Julius O. Smith III, W3K Publishing, 2010, ISBN 978-0-9745607-2-4
Copyright © 2024-06-28 by Julius O. Smith III
Center for Computer Research in Music and Acoustics (CCRMA),   Stanford University
CCRMA